First exercises in rotation: Newton's Second Law and Rotational Inertia

At this point in AP Physics 1 for upperclassmen, students are used to the idea that a new topic brings new facts and equations, which are then applied to make predictions to be verified experimentally.  Rotation provides an opportunity to introduce the topic directly with individual laboratory exercises, especially since the concepts of inertia, force, and acceleration are already familiar.  We are simply applying the concepts to a rotational setting.  

I spent way too long creating three versions of the pictured setup.  An object of mass between 10-200 g hangs from a string, which is passed over a pulley and wrapped around an axle.  The axle is attached to a wide and massive disk.  The hanging object is released from rest, causing the disk to accelerate rotationally.  I have the expensive PASCO version; a similar apparatus can be created for just a few dollars from PVC pipe placed over a ringstand, kind of as shown on problem 3 of the 2001 AP Physics C Mechanics exam.

A set of seven exercises is available for you to download and try out at this link.  I hand out the first to everyone, and help each student create an angular velocity vs. time graph for the rotating disk.  Then, each student individually, with his own unique graph, answers each of the questions, getting my approval before moving on to the next one.

Creating that ω vs. t graph requires some ingenuity.  The simplest way is to use the smart pulley and photogate; in fact, the PASCO apparatus provides a screw specifically aligned so that the photogate can easily be placed just right.  Problem is, I have Vernier photogates, which conveniently don't fit with the PASCO equipment.  D'oh.

So I set up a photogate vertically, a bit more than one disk-radius away from the rotational axis.  I cut a piece of paper such that its width was a known angle -- I calculated that with the 11.7 cm-radius disk, a 0.9 cm width paper subtends an angle of 0.08 radians.  Don't ask me why I chose that value -- I did, it works, and now I ain't gonna do any more cutting and taping.  (You can check my math, though.   Using x = rθ, 0.9 cm does in fact equal 11.7 cm times 0.08 radians.)  

Next, I set up my labquest to read the photogate in "gate" mode, with a "distance" of 0.08 m.  Thus, the labquest thinks it's making a linear velocity vs. time graph in units of m/s.  I fooled it, though -- it's really making an angular velocity vs. time graph, in units of radians per second.

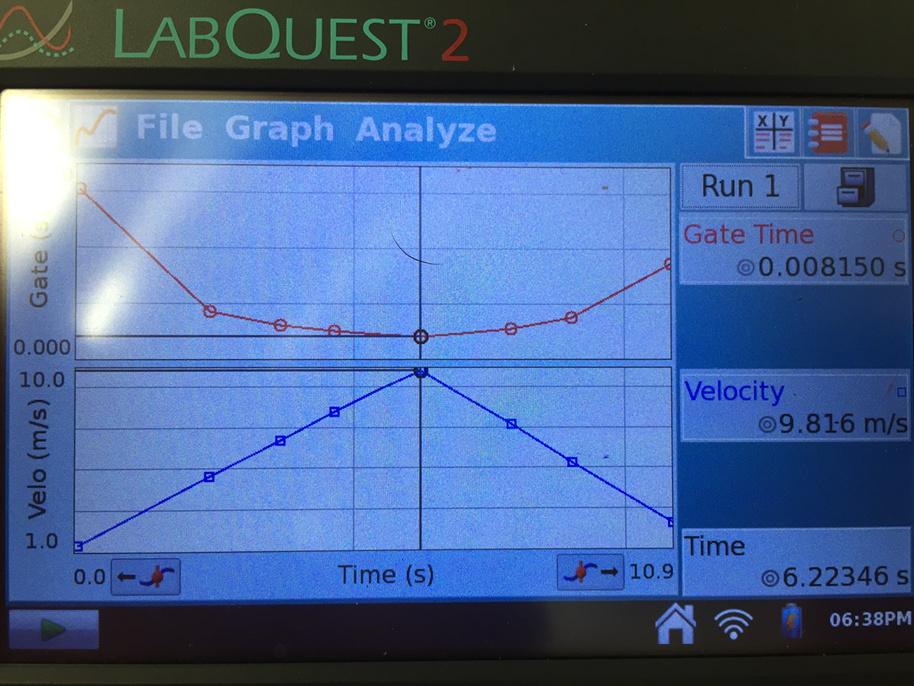
Once I finished the setup, the data collection was a breeze.  Students on their own could create beautifully linear ω vs. t graphs, as shown to the right.  Then they figured out to take the slope to determine the angular acceleration; they calculated torque with force times lever arm; and they calculated the rotational inertia of the disk.  I deliberately had half the class using the gray disk by itself, and the other half using the gray disk with a heavy ring on top; sure enough, the half of the class with the extra heavy ring calculated a significantly larger rotational inertia.

The subsequent exercises each ask the student to redo the experiment, changing one of three things:

(1) Changing the net torque by changing the hanging object's weight

(2) Changing the net torque by changing the lever arm

(3) Changing the rotational inertia by adding or removing the heavy ring

In each case, students predict the new angular acceleration using semi-quantitative reasoning, and then measure to verify their prediction.  Results are generally accurate well within 10% of the predictions.

Postcript:  Throughout these exercises, I'm making the approximation that the tension in the rope that provides the torque is equal to the weight of the hanging object.  This is not precise -- since the hanging object is accelerating downward, the tension in the rope is a big less than the weight of the hanging object.  So what.  When I do the precise calculation, I find that the effective rotational inertia of the whole system is increased by mr², where m is the hanging object's mass and r is the lever arm of 1-2 cm.  Since that is SO much less than the rotational inertia of the disk itself (where the disk's mass is significantly larger than m and the disk's radius is ten times larger than r), I've made a good assumption.  Eventually, when someone asks about the string's tension not being truly equal to mg (as someone did on Thursday), I can have a nice conversation.